Asymptotic Notation
Asymptotic notation is a way of expressing the cost of an algorithm. Goal of Asymptotic notation is to simplify Analysis by getting rid of unneeded information
Following are the asymptotic notation:
| Big–Oh Notation (O) : |
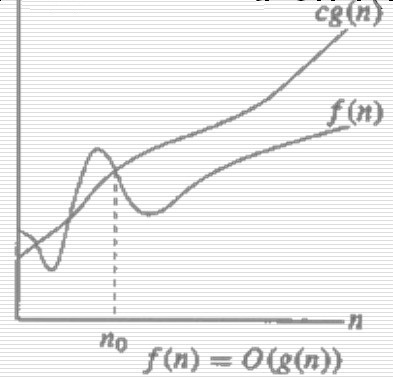
| >> O(g(n)) = { f(n) : there exist positive constants c and n0 such that 0 < f(n) < c*g(n) for all n > n0 }.
>> It is asymptotic upper bound.
>>The function f(n) = O(g(n)) iff there exist positive constants c and n0 such that f(n) ≤ c * g(n) for all n, n ≥ n0.
>> The statement f(n) = O(g(n)) states only that g(n) is an upper bound on the value of f(n) for all n, n ≥ no.
>> Eg :
1. 3n + 2 = O(n)
3n + 2 ≤ 4n for all n ≥ 2.
2. 3n + 3 = O(n)
3n + 3 ≤ 4n for all n ≥ 3.
3. 100n + 6 = O(n)
100n + 6 ≤ 101n for all n ≥ 6.

|
| Omega Notation (Ω) |
| >> Ω (g (n)) = { f(n) : there exist positive constants c and n0 such that 0 < c * g(n) < f(n) for all n > n0 }
>> Asymptotic lower bound.
>> The function f(n) = Ω(g(n)) iff there exist positive constants c and n0 such that f(n) ≥ c * g(n) for all n, n ≥ n0.
>> The statement f(n) = Ω(g(n)) states only that g(n) is only a lower bound on the value of f(n) for all n, n ≥ no.
>> E.g.
1. 3n + 2 = Ω(n)
3n + 2 ≥ 3n for all n ≥ 1.
2. 3n + 3 = Ω(n)
3n + 3 ≥ 3n for all n ≥ 1.
3. 100n + 6 = Ω(n)
100n + 6 ≥ 100n for all n ≥ 0. |
| Theta Notation (Θ) |
| >> Θ(g(n)) = { f(n) : there exist positive constants c1 and c2 and n0 such that 0 < c1 * g(n) < f(n) < c2 * g(n) for all n > n0 }
>> The function f(n) = Θ(g(n)) iff there exist positive constants C1, C2 and n0 such that C1 * g(n) ≤ f(n) ≤ C2 * g(n) for all n, n ≥ n0.
>> E.g.
1. 3n + 2 = Θ(n)
3n + 2 ≥ 3n for all n ≥ 2.
3n + 2 ≤ 4n for all n ≥ 2.
So, C1 = 3, C2 =4 & n0 =2.
>> The statement f(n) = Θ(g(n)) iff g(n) is both an upper and lower bound on the value of f(n).  |
| Little oh Notation (o) |
| >> o(g(n)) = { f(n) : for any positive constant c>0 , there exists a constant n0 such that 0 < f(n) < c * g(n) for all n > n0 }
>> We use o notation to denote an upper bound that is not asymptotically tight.
>> The definitions of O-notation and o-notation are similar. The main difference is that in f(n) =O(g(n)), the bound 0 < f(n) < c*g(n) holds for some constant c>0 but in f(n) =O(g(n)), the bound 0 < f(n) < c *g(n) holds for all constants c > 0. |
| Little omega Notation (w) |
| >> w(g(n)) = { f(n) : for any positive constant c>0 , there exists a constant n0 such that 0 < c * g (n) < f(n) for all n > n0 }
>> We use w notation to denote an lower bound that is not asymptotically tight. |